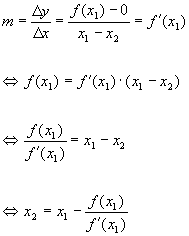09.03.02

Nicht immer sind die zu bestimmenden Nullstellen von ganzrationalen Funktionen ganzzahlig, so dass man mit der Polynomdivision nicht sinnvoll arbeiten kann. Erst recht gilt dies, wenn man Nullstellen von nichtrationalen Funktionen wie Exponentialfunktionen oder trigonometrischen Funktionen sucht.

Man muss die Nullstellen in diesem Fall näherungsweise bestimmen; ein elegantes und sehr effektives Verfahren hierzu ist das

Newtonsche Näherungsverfahren.

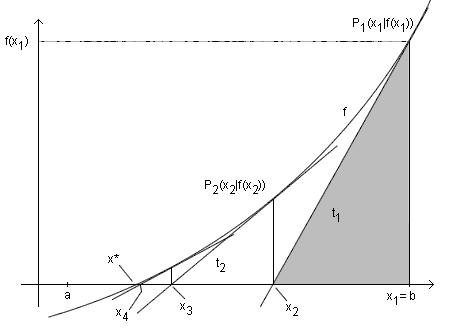
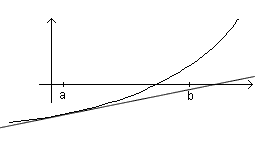
Man geht bei diesem Verfahren davon aus, dass ein Intervall [a;b] bekannt ist, in dem die gesuchte Nullstelle x* liegt. Man wählt nun eine geeignete Intervallgrenze als erste Näherung und damit als Startstelle x₁ für das Verfahren; im Beispiel ist es b.

Betrachtet man nun das grau unterlegte Steigungsdreieck, so ist die Steigung der darin enthaltenen Tangente t₁ gleich der Steigung des Graphen von f in P₁ und damit gilt:

m = f '(x₁).

Durch Umformen erhält man nun die gegenüber x₁ verbesserte Näherung x₂ .

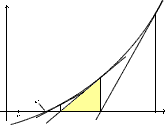
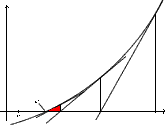
Das Steigungsdreieck zum zweiten Schritt sähe dann so aus:

Zum dritten Schritt:

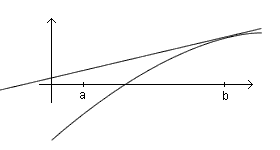
Bemerkung zum Begriff „geeignete Startstelle“:

In ungünstigen Fällen schneidet die Tangente t₁ die x-Achse außerhalb des Intervalls [a;b].

In den beiden Fällen gilt aber    f(x₁) · f''(x₁) < 0

Überprüft man die Startstelle darauf, ob diese Bedingung erfüllt ist, beobachtet man fast immer, dass sich die Näherungswerte in einer Richtung der Stelle x* nähern.